ABOUT US
EST. 2023
The Team:
Sharnel Alvez
R Jay Berano
Justine Faith Daga
Nikki Demition
Archie Ferrera
Clarence John Perez
Sabina Jasmin Rapanan
Shannon Lexi Santos
u-Mathter is a site where everything math is made easy. We offer easy-to-follow instructions, easy-to-comprehend definitions, and easy-to-do solutions. With us, you don't need to have the feeling of burden you always carry in your life with math. We are here to help you, because for us, you and your betterment is what MATHters.

DERIVATIVES
One of the most important tools in differential calculus is derivative. Derivatives provide us with a flexible means to measure precise rates of change, which is fantastic!
Simply defined, derivatives show us the instantaneous rate of change at a specific point on a function's graph. That means we can easily capture a rather robust piece of information (depending on the level of math you're conducting!).
Furthermore, knowing how to determine derivatives allows us to more properly represent things like velocity, force, acceleration, and more — so they're not just for homework. Derivatives are essential to the inner workings of so many things around us.
GENERAL RULES
CONSTANT RULE
The constant rule states that the derivative of any constant function is always zero
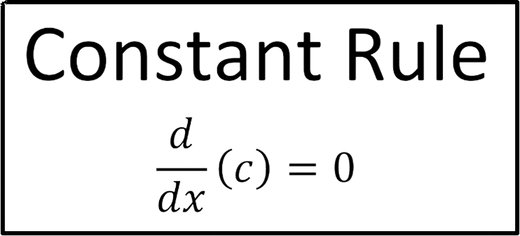
CONSTANT MULTIPLE RULE
The constant multiple rule states that if c is a constant and f(x) is a differentiable function, then:

POWER RULE
The power rule states that if n is any real number, then the derivative is:

SUM AND DIFFERENCE RULE
The sum and difference rule for derivatives states that if f(x) and g(x) are both differentiable functions, then:

PRODUCT RULE
The product rule states that if f(x) and g(x) are both differentiable functions, then the derivative of their product also exists.

QUOTIENT RULE
The quotient rule states that if f(x) and g(x) are both differentiable functions and g(x) does not equal zero, then the derivative of their quotient also exists.
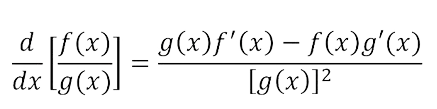
CHAIN RULE
The constant multiple rule states that if c is a constant and f(x) is a differentiable function, then:
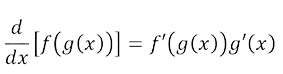
TRIGONOMETRIC FUNCTIONS DERIVATIVES
Differentiation of trigonometric functions is a mathematical procedure used in trigonometry to determine the rate of change of trigonometric functions with respect to a variable angle. The quotient rule can be used to differentiate trigonometric functions using the derivatives of sin x and cos x. The differentiation formulas of the six trigonometric functions are listed below:
Derivation of sin x: (sin x)' = cos x
Derivative of cos x: (cos x)' = -sin x
Derivative of tan x: (tan x)' = sec^2x
Derivation of sin x: (sin x)' = cos x
Derivative of cos x: (cos x)' = -sin x
Derivative of tan x: (tan x)' = sec^2x
CONTACT US
If you have any suggestions and clarifications regarding the given information in this website, please do not hesitate to contact us using the feedback form that you can access by clicking the button below.
Here in u-Mather, we make sure that complex lessons were expressed and explained in simplest form. Hope you learned something today!
EST. 2023
